Door: drs. Neil van der Veer
Oké, het is natuurlijk praten voor eigen parochie. Maar ik verbaas me simpelweg vanuit mijn professie als onderzoeker dat er nu zo’n verbazing is over het grote verschil tussen de verkiezingsuitslag versus de resultaten van de eerdere opiniepeilingen. Als mens verbaast mij de uitslag ook, maar vanuit de regels van statistiek is het vrij goed verklaarbaar. Hieronder zet ik een aantal berekeningen uiteen.
Het belangrijkste argument is dat er niet met hetzelfde systeem wordt gewerkt.
De opiniepeilingen zijn gebaseerd op inwonersaantallen. En of je nu een inwonersaantal van 10 miljoen hebt of van 320 miljoen, om de stemming te peilen heb je aan 1.000 mensen te ondervragen vaak echt genoeg.
De verkiezingsuitslag is echter gebaseerd op kiesmannen. En juist die verhouden zich niet 1-op-1 met de inwonersaantallen. En als je een a-selecte steekproef over het gehele land neemt, zoals de huidige opiniepeilingen, dan komen er grote verschillen uit. Om deze stelling te onderbouwen geef ik hieronder een fictief en een reëel voorbeeld.
Eerst een fictief en wellicht ongenuanceerd voorbeeld.
Fictief
Stel je hebt 3 staten met in totaal 170 inwoners. De verhouding ziet er als volgt uit.

Het aantal kiesmannen in deze drie staten is in totaal 65 kiesmannen en als volgt verdeeld:
- Staat A: 10 kiesmannen;
- Staat B: 25 kiesmannen;
- Staat C: 30 kiesmannen.
Stel dat een kandidaat in staat 1 en 2 wint met 60 procent, maar in staat C verliest met 20 procent. Qua inwonersaantallen zou je dan het volgende krijgen:
- Staat A: 6 inwoners (60%);
- Staat B: 36 inwoners (60%;
- Staat C: 20 inwoners (20%).
In totaal zal je dan over het geheel 62 inwoners hebben en dat zou een uitslag van 36 procent betekenen. Feitelijk zou de andere kandidaat ruim winnen.
Maar nu komt het: qua kiesmannen komt er een totaal andere uitslag uit.
- Staat A: gewonnen, dus 10 kiesmannen;
- Staat B: gewonnen, dus 25 kiesmannen;
- Staat C: verloren, dus 0 kiesmannen.
In totaal heb je dan 35 kiesmannen. En dat betekent 54 procent van alle kiesmannen. Een compleet andere uitslag dus.
Dit voorbeeld is uiteraard fictief en redelijk ongenuanceerd. Daarom nu een reëel voorbeeld gebaseerd op 5 willekeurige staten in Amerika. In dit voorbeeld zie je dat California 36 miljoen inwoners heeft en 55 kiesmannen te verdelen heeft. Montana heeft met een kleine miljoen inwoners 3 kiesmannen. Hier zie je al een verschil in verhoudingen. Montana is 38 keer zo klein qua aantallen als California, maar heeft ‘maar’ 18 keer zo weinig kiesmannen.
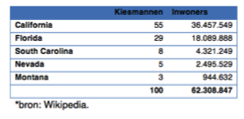
En als je dan vervolgens de verdeling qua percentages kiesmannen afzet tegen de verdeling op basis van de inwonersaantallen, dan zie je waar de schoen wringt. Je ziet dat de kleinere staten in onderstaande tabel oververtegenwoordigd zijn qua kiesmannen. Je ziet bij een staat als Montana dat de relatieve afwijking zelfs (bijna) 50 procent is.
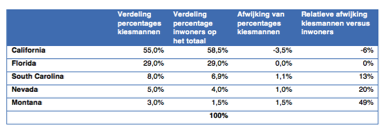
Resumerend kun je dus stellen dat je niet uit kunt gaan van een algemeen gemiddelde over heel Amerika. En dat is precies gebeurt bij relatief veel peilingen: er wordt niet uitgegaan van een stemming per staat, maar een opinie over geheel Amerika. De peilingen zijn daarmee niet in lijn met het stelsel zelf.
Spelen er nog andere effecten mee? Zeker. Ik zie bijvoorbeeld dat er bij een aantal peilingen vooral gebruik wordt gemaakt van telefonisch onderzoek. Telefonisch onderzoek is heel goed als het gaat om een hoge respons en het doorvragen over bepaalde onderwerpen. Maar als het gaat om precaire onderwerpen zoals stemmen is online onderzoek anoniemer en dus minder sociaal wenselijk. Ook heb je nog effecten op de dag zelf, welke moeilijk te meten zijn. Toch kun je door het inbouwen van zogenaamde ‘zekerheidsvragen’ wel een betere voorspelling doen.
Hoe dan wel?
Een oplossing is een zogenaamde gestratificeerde steekproef (aselect). Of in normale taal: 50 aparte steekproeven binnen elke staat met een voldoende grootte qua steekproef. Dan krijg je de stemming binnen elke staat en deze kun je vervolgens extrapoleren naar het aantal kiesmannen. En dus naar een projectie op de verkiezingsuitslag. Maar goed, daar zitten natuurlijk ook budgettaire kaders aan. Een steekproefmarge van 5% is gangbaar bij dergelijk onderzoek en om een betrouwbaarheidsniveau van 95 procent te halen kom je dan al snel op 50 staten maal n=400. En dan praat je over een steekproef van n=20.000. Dat heeft geen enkele media noch politieke partij gedaan vrees ik.
Achteraf zullen ze nog wel eens nadenken over onderstaande zin..
Het ‘weten’ kost geld, het ‘niet weten’ kost kapitalen…
